Blue Anarchy >> Navigating Your Dreams By The Stars
Introduction
These days, it's possible to buy a compact GPS receiver for less than a sextant. No bulky sight reduction tables or nautical almanacs are required, you can determine your location instantly, and some will even plot your course on an electronic map. With that kind of technology available, it might seem like a waste of time to read a pamphlet on celestial navigation. What's the point, anyway?
Of course, there are all the standard excuses that old mariners give for holding on to their sextants: what if the batteries in your GPS die, or what if the GPS satellites go offline? Those are good practical reasons, but I think there is more to the value of celestial navigation. There is convenience in the quick glance at a glowing GPS readout, but that convenience might only serve as another blow for alienation. What is that vapid stare compared to the feeling of salt spray on your face while measuring the declinations of celestial bodies throughout the heavens? What about the awareness and anticipation of that perfect moment at twilight, just right for taking sights, when the waning light still illuminates the horizon and the planets are becoming visible in the sky? What about the day to day knowledge of how the planets are moving across the heavens, when exactly local noon occurs, and the intrinsic feeling that you are navigating your dreams by the stars?
Certainly GPS is nice to have, but for me celestial navigation is wrapped up in DIY and a connectedness with the world which strikes back against spectatorship and alienation. If you feel potential for the same, hopefully this pamphlet will help you along the way.
First Principles
The Sextant: A tool for measuring angles between observable objects. In the context of celestial navigation, those bodies are most often a celestial object (the sun, a star, a planet) and the horizon.
Geographical Position (GP):
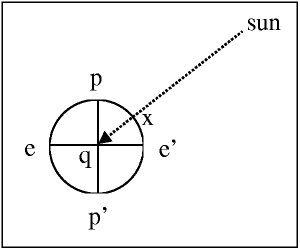 The point on earth that a celestial body is directly above. If you draw a line from the center of the earth to a celestial body, the point where that line intersects the earth's surface is the geographical position. GP is measured by 'declination' and 'hour angle'.
The point on earth that a celestial body is directly above. If you draw a line from the center of the earth to a celestial body, the point where that line intersects the earth's surface is the geographical position. GP is measured by 'declination' and 'hour angle'.
Ex: Here, 'x' is the GP of the sun.
Declination: The declination of a celestial object is just the latitude of its GP. Declination is measured exactly as latitude is: in degrees north or south of the equator. The declination of the sun moves from 23˚N (Tropic of Cancer) to 23˚S (Tropic of Capricorn) throughout the year.
Hour Angle: Hour angle is the 'longitude' complement to declination when measuring GP. Greenwich Hour Angle (GHA) is the amount of time that has elapsed since a celestial body passed the Greenwich meridian. If you're standing on the Greenwich meridian and the sun is directly south, its GHA is 0. Two hours later, its GHA will be two hours. Its GHA will continue to grow through 23 hours until noon the next day, when it will become zero again. GHA can be measured in degrees past the Greenwich meridian as well (up to 360˚). So hour angle is different from longitude in two ways: it can be measured in time, and when it is measured in degrees it goes up to 360˚ in the westerly direction, instead of 180˚ east or west.
Local Hour Angle: Hour Angle doesn't have to be measured from the Greenwich meridian. When it is measured from the meridian that you (the observer) are on, it is known as the Local Hour Angle (LHA). Simple equations for translating GHA to LHA:
When east of Greenwich: LHA = GHA + observer's longitude
When west of Greenwich: LHA = GHA - observer's longitude
The Nautical Almanac: Published annually, these need to be updated every year. They give GPs (in GHA and declination) of celestial bodies at every second throughout the year. They also hold additional information about sunrise, sunset, and the phases of the moon.
The Zenith: This is the point immediately above your head. It makes an angle of 90˚ between you and the horizon.
Altitude: The angle between a celestial object, an observer, and the horizon. From your perspective, this is the height of a celestial object above the horizon.
 Zenith Distance:
The complement to altitude. Ex: altitude + zenith distance will always equal 90˚.
Zenith Distance:
The complement to altitude. Ex: altitude + zenith distance will always equal 90˚.
Azimuth: The bearing (true not magnetic) from an observer to a heavenly body.
The Theory
Zenith Distance And Latitude
It turns out that you can learn some interesting things from zenith distance. In this diagram, two parallel rays from the sun hit the earth. One at an observer's position, and one at the sun's GP:
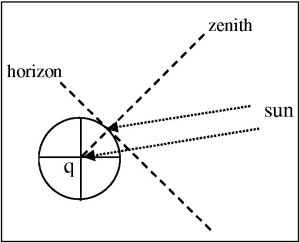 What's interesting is that the angle between the zenith and the first ray at the surface of the earth is the same as the angle between the zenith and the second ray at the center of the earth. This means that the zenith distance which you observe is the same number of degrees as the distance between the GP and you. Since 1' = 1 nautical mile, zenith distance * 60 = the distance between you and the GP of the object you're observing.
What's interesting is that the angle between the zenith and the first ray at the surface of the earth is the same as the angle between the zenith and the second ray at the center of the earth. This means that the zenith distance which you observe is the same number of degrees as the distance between the GP and you. Since 1' = 1 nautical mile, zenith distance * 60 = the distance between you and the GP of the object you're observing.
If the object that you're observing happens to be directly above your meridian of longitude, that distance + the object's declination = your parallel of latitude. Declination is something that you can look up in a nautical almanac for most celestial bodies at any given moment, and the sun will predictably cross your meridian of longitude at local noon. This means that you can easily determine your latitude at noon every day.
Determining Longitude At Noon
Now that we know how to determine our latitude at noon, it would be nice if we could also discover our longitude. As the sun approaches its high point in the sky, begin to take a series of sights, marking the time of each sight taken. The altitude you measure will get larger, hang for a minute or so, and then begin to get smaller. Wait until the sun falls to the altitude of your very first site, determine the difference in time between the last and first site, add half that to the time of the first site, and that was the exact moment of local noon. The sun's GP moves 15˚ every hour, so look up the time of local noon at Greenwich in a nautical almanac, determine the number of minutes between then and now, divide that by 4 to get the number of miles between your longitude and Greenwich, and divide that by 60 to get your longitude in degrees. Now we have a method for easily determining both our latitude and longitude at local noon.
Position Circles
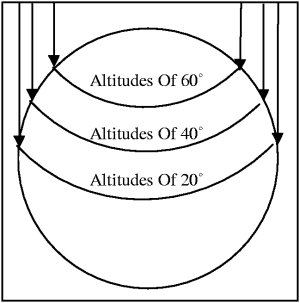 Let's say that you use a sextant to take a sight of the sun, and its altitude is 90˚ (your zenith). With absolute certainty, there is only one place on the earth that you could possibly be: the sun's GP. As the sun continues to move across the sky, however, its altitude will lessen. As this happens, your number of possible positions will grow into a 'position circle' with the sun's GP at its center, and a number of equidistant points around it. Given an observed altitude, all you know is that you're somewhere on the position circle. The circle gets larger and larger the lower the observed altitude.
Let's say that you use a sextant to take a sight of the sun, and its altitude is 90˚ (your zenith). With absolute certainty, there is only one place on the earth that you could possibly be: the sun's GP. As the sun continues to move across the sky, however, its altitude will lessen. As this happens, your number of possible positions will grow into a 'position circle' with the sun's GP at its center, and a number of equidistant points around it. Given an observed altitude, all you know is that you're somewhere on the position circle. The circle gets larger and larger the lower the observed altitude.
Position Lines
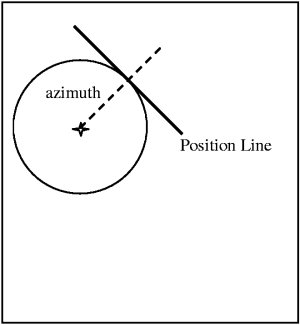 The trick is to narrow the number of possible positions on the Position Circle by plotting your azimuth to the celestial object. If the celestial object is to the SW of the observer, than the observer must be on the NE portion of the Position Circle. There is no way, however, to obtain an azimuth so accurate that you can determine your exact position on the circle. The best you can do is draw a line at right angles to the azimuth, knowing that you are somewhere on the tangent of the position circle and that line.
The trick is to narrow the number of possible positions on the Position Circle by plotting your azimuth to the celestial object. If the celestial object is to the SW of the observer, than the observer must be on the NE portion of the Position Circle. There is no way, however, to obtain an azimuth so accurate that you can determine your exact position on the circle. The best you can do is draw a line at right angles to the azimuth, knowing that you are somewhere on the tangent of the position circle and that line.
Spherical Triangles
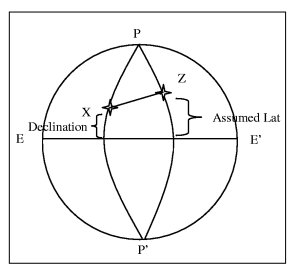 Drawing a position circle isn't easy. There are enormous distances involved, so we'd need a really big chart and a really big compass to draw the required circle with the celestial body's GP at the center. In order to get the Position Line that we want, we use spherical triangles to find what's known as an Intercept. We have a celestial body's observed altitude and need to know where we are. But when using spherical triangles, we pretend that we don't have the celestial body's altitude and do know where we are. The assumed latitude and longitude are called an 'assumed position' (AP).
Drawing a position circle isn't easy. There are enormous distances involved, so we'd need a really big chart and a really big compass to draw the required circle with the celestial body's GP at the center. In order to get the Position Line that we want, we use spherical triangles to find what's known as an Intercept. We have a celestial body's observed altitude and need to know where we are. But when using spherical triangles, we pretend that we don't have the celestial body's altitude and do know where we are. The assumed latitude and longitude are called an 'assumed position' (AP).
Here 'Z' is the observer's assumed latitude, and 'X' is the GP of the celestial body. We know the length of PZ = 90˚ - the assumed latitude. We know the length of PX = 90˚ - the celestial body's declination. We know that the angle ZPX is the Local Hour Angle. Since we know two sides and an angle of a triangle, we can use spherical trigonometry to solve for the length of ZX and the other two angles. 90˚ - ZX = altitude, or what's known as the Calculated Altitude. The angle PZX will be the azimuth. Had the assumed position been a perfect guess, the calculated altitude would be the same as the observed altitude. If it's not, the difference between the calculated altitude and observed altitude is the Intercept, as specified in nautical miles.
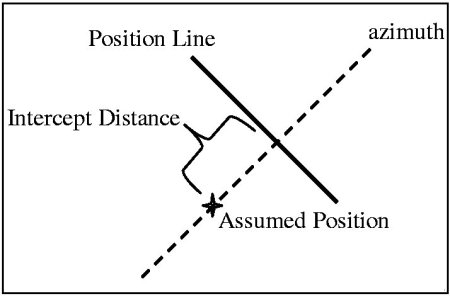
Plotting An Intercept
Drawing a position line is now as easy as plotting the calculated azimuth through the assumed position, walking the value of the Intercept up the azimuth line, and drawing the position line at a right angle. We're somewhere on that line.
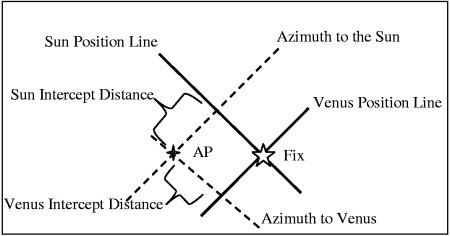
The Fix
This position line stuff is interesting, but it'd be a hell of a lot nicer if we could find out exactly where we are. The solution is to plot multiple position lines and see where they intersect. There are two ways to do this.
Multiple Sights
The best way to get a fix is to take multiple sights off multiple celestial objects. This is possible during the day when the moon has already risen, or at twilight when the planets are already visible. It is, of course, possible at night when all the stars are in the sky -- but it might be difficult to see the horizon then.
The Running Fix
If all you have is the sun, it's possible to take a Running Fix. The idea is to plot a position line off the sun, wait for your azimuth to the sun to change (a few hours usually), plot a second position line, and then advance the first position line the distance you've traveled. If you've traveled 45nm at a bearing of 67˚ between the first and second sight, draw a line at 67˚ through any point on the first position line, measure up 45nm, and re-plot the first position line at that point. Your fix is where the advanced and second position lines intersect.
The Practice
The steps for plotting a position line are:
- Use a sextant to observe the altitude of a celestial body.
- Using the exact time of your observation, look up the GP for that celestial body in the Nautical Almanac.
- Assume a position.
- Solve the spherical triangle between your assumed position, the celestial body's GP, and the closest pole.
- Use the results of the spherical triangle to determine the difference between the calculated altitude and your observed altitude.
- Plot that difference as an intercept on a chart.
Using The Sextant
Look through the sextant at the horizon and adjust the sextant's index arm until the celestial body is visible in the silvered portion of the view finder. Slowly adjust the index arm until the bottom of the celestial object is touching the horizon. Either call out to a time keeper, or quickly look at your watch. Record the time and altitude.
It is now necessary to correct the observed altitude for instrument error, our height above sea-level, refraction, and semi-diameter.
To account for instrument error, slide the index arm to 0˚ and look through the view finder. If the sextant has no error, the horizon should be perfectly aligned in the silvered and unsilvered portions of the view finder. If they are not aligned, adjust the index arm until they are. Subtract the number of minutes on the index arm from the observed altitude to get an observed altitude corrected for instrument error.
To account for height above sea level, estimate the height of the boat and the height of the sextant above deck (approximately the height of the observer). In the Nautical Almanac, on the right side of the 'Altitude Correction Tables -- Moon' page, there is a table labeled 'Dip'. Lookup your estimated height, and subtract the value in the 'Corr' column from the observed altitude to get observed altitude corrected for height above sea level.
To account for refraction and semi-diameter, look at the 'Altitude Correction Tables' page in the Nautical Almanac. Since you measured the lower limb against the horizon, look up the observed altitude in the table and subtract the 'lower limb' column from the observed altitude to get observed altitude corrected for refraction and semi-diameter.
Combining all of these corrections gets you a usable observed altitude (abbreviated Ho).
Finding The GP Of A Celestial Object
Each page in the body of the Nautical Almanac provides information for three days. The tables list the GHA and declination of Venus, Mars, Jupiter, Saturn, the Sun, and the moon for every hour. Find the page for the day you took the sight, then record the GHA and declination for the hour in which you took the sight. Also note the value of 'd' (located at the bottom of the Sun and planets columns, but in-line in the moon column).
At the back of the Nautical Almanac, there are a series of pages labeled 'Increments And Corrections.' Each page has a table for a given minute, with each row containing values for that second. Find the page for the minute in which you took your observation, and add the value in the column for the second in which you took your observation to the previously looked-up GHA. Next, look at the right three columns on the same page. These are actually one long table. Find the value of 'd' on the left side, and record the value on the right side as the 'declination correction.' You either add or subtract this to the previously looked-up declination depending on whether it is in a place where the values of the column are either increasing or decreasing. You now have the GHA and declination which specify the GP of the celestial object in the moment that you observed it.
Now you know that you're somewhere on a circle that has a radius of (90˚ - observed altitude) x 60 nm with the GP at its center. But we can do better.
Assuming A Position
For reasons which will soon become clear, your assumed position needs to be a whole number of degrees in latitude, and a longitude which makes the LHA of the celestial body a whole number of degrees as well. Choosing your AP latitude is as easy as picking the nearest latitude degree to your Deduced Reckoning position. Choosing your AP longitude is as easy as picking the nearest longitude to your Deduced Reckoning position, which when added or subtracted to GHA will produce an even LHA.
Ex: If your DR position is 27˚34'.4N, 08˚25'E and the GHA you just looked up is 337˚01', your AP Lat would be 27˚ and your AP Long would be 7˚59'E, such that the LHA is an even 345˚00'.
Solving The Spherical Triangle
As it turns out, spherical trigonometry is not the kind of math that we can do on our fingers. As such, we use a series of tables (called Sight Reduction Tables) to help us solve the spherical triangle. Each row in the tables contains a previously worked out solution to a different permutation of spherical triangle. This is why the LHA and AP Lat must be a whole number of degrees: there are only so many possible permutations that the tables can contain.
Each page for a given AP Latitude has solutions for a range of GP declinations that are either of 'same' or 'contrary' name. If the AP latitude and GP declination that you're looking up are in the same hemisphere, then you should look on the 'same name' page. Otherwise, use the 'contrary name' page. Look in the row for the degree of GP declination, under the column of your calculated LHA. Record the Calculated Altitude (Hc), the value of 'd', and the azimuth. In the back of the book, in the table labeled 'Correction To Tabulated Altitude For Minutes Of Declination,' look up the row containing the value of 'd' under the column containing the minutes of your GP declination. Add this value to the previously looked-up Calculated Altitude (Hc) to get the correct value for Hc.
Plotting The Intercept
The difference between the Calculated Altitude and Observed Altitude is the intercept. Draw a line through the AP on a bearing of the calculated azimuth, measure off the intercept distance along the azimuth line, and draw a line at a right angle to the azimuth line at that point. You now have a position line.
This may seem like a series very confusing operations, but really it's just 8 addition or subtractions and 4 table lookups. Attached is a worksheet to help you work through a sight, step-by-step.
